


Next: Ground truth: verifying the
Up: Estimation with unknown exposure
Previous: The general case: multiple
It is expected that pixel values near the middle of
their range in the image will change more rapidly
for a given change in exposure than pixel values close to the extremes.
For example, when a pixel is saturated (e.g. 255 in the case of an
eight bit camera) no additional light will change the pixel value.
Therefore, we expect that the midtones in the image will give greater
certainty in estimating 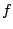 than will the shadows and highlights.
This intuition is made formal by the
so-called certainty functionsmannwyckoff[3],
which are the derivatives of the response functions.
than will the shadows and highlights.
This intuition is made formal by the
so-called certainty functionsmannwyckoff[3],
which are the derivatives of the response functions.
The certainty functions may therefore be used to weight the columns of
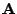 , and the corresponding entries of
the vector
, and the corresponding entries of
the vector 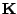 , when solving for
, when solving for
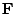 :
A_w=A (w1)
:
A_w=A (w1)
A_w^TA_wF - A_w^TK_w = 0
where 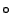 denotes Hadamard
multiplication5,
denotes Hadamard
multiplication5,
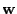 is a column vector in which each entry is made up of
is a column vector in which each entry is made up of
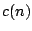 where
where 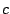 is the certainty function, and
is the certainty function, and 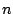 is the column index
in which the quantity
is the column index
in which the quantity 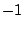 appears for that row.
appears for that row.
In practice, we do not know the response function (this is
the very entity we are trying to estimate) so we
also do not know a-priori, its derivative,
the certainty function, which we need to use in the weighting.
Figure 7:
(a) One of 19 differently exposed pictures
of test pattern.
(b) Each of the 19 exposures produced 11 ordered pairs in a plot
of 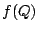 as a function of
as a function of 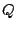 .
(c) Shifting these 19 plots left or right by the appropriate
.
(c) Shifting these 19 plots left or right by the appropriate 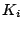 allowed them all to line up to produce the ground truth
known-resonse function
allowed them all to line up to produce the ground truth
known-resonse function 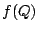 .
.
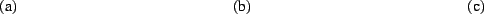 |
However, we can use a certainty function
that has the general shape of the derivative of a typical response
function. It has been found that the solution 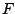 is not particularly sensitive to the shape of the certainty function.
A Gaussian weighting is generally used.
If desired, once
is not particularly sensitive to the shape of the certainty function.
A Gaussian weighting is generally used.
If desired, once 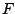 is found,
is found, 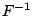 can be differentiated and
used as the certainty function to weight the columns of
can be differentiated and
used as the certainty function to weight the columns of 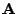 to
re-estimate
to
re-estimate 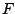 . This procedure can be repeated again (e.g.
giving rise to an iterative estimation of
. This procedure can be repeated again (e.g.
giving rise to an iterative estimation of 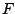 ).
).



Next: Ground truth: verifying the
Up: Estimation with unknown exposure
Previous: The general case: multiple
Steve Mann
2002-05-25
![]() , and the corresponding entries of
the vector
, and the corresponding entries of
the vector ![]() , when solving for
, when solving for
![]() :
A_w=A (w1)
:
A_w=A (w1)
![]() denotes Hadamard
multiplication5,
denotes Hadamard
multiplication5,
![]() is a column vector in which each entry is made up of
is a column vector in which each entry is made up of
![]() where
where ![]() is the certainty function, and
is the certainty function, and ![]() is the column index
in which the quantity
is the column index
in which the quantity ![]() appears for that row.
appears for that row.